Multi-Scale Modelling of Electromechanical Coupling in Perovskite-Based Ferroelectric Materials and Composites

14 December 2022

Ferroelectric materials have great importance for modern society with a wide range of applications in electronic devices such as actuators, transducers and sensors. The important characteristics of ferroelectrics is a phase transition with the Curie temperature as the transition temperature. When the temperature decreases through the Curie point, a ferroelectric crystal undergoes a structural phase transition from a paraelectric cubic phase to a ferroelectric phase.

Introduction

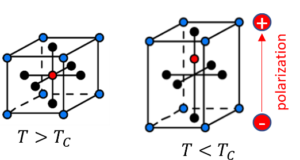
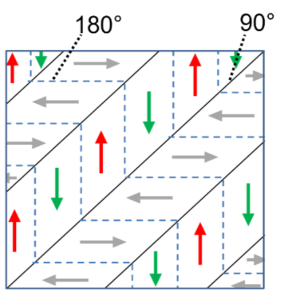
Fig. 1: Unit cells of a ferroelectric perovskite in the cubic paralelectric state (left) and the tetragonal ferroelectric state (right), which is associated with a shift of the centers of positive and negative electric charge, leading to polarization.

Fig. 2: Schematic of the stable evolving domain pattern with charge-free 90° (solid) and 180° walls (dashed)

A common feature of a ferroelectric phase is the spontaneous alignment of electric dipoles in a domain structure, where every single domain possesses a constant polarization direction. The interface between the domains is called domain wall. For example, in a perovskite ferroelectric material BaTiO₃ with polarizations along (100) and (010), the domains are aligned at and angle of 180° and 90°.

Phase-field models have been established as efficient tools to study the evolution of domain structure in ferroelectrics. The main feature of these models is that different polarization domains are described by a phase-field variable, as a spatial and temporal changing field. This parameter, which distinguishes different domains, is called order parameter. For ferroelectric domain evolution, polarization is usually regarded as the order parameter. The evolution of the polarization is subjected to the following equation:

β∂P/∂t = – δF/δP

where β is the kinetic coefficient, δ is the functional derivative of the total free energy density F with respect to the polarization P. In the ferroelectric community, this equation is referred to as time-dependent Ginzburg-Landau (TDGL) equation.

Scope of Work

In this topic, we implement the TDGL and governing constitutive equations using semi-implicit Fourier spectral method in open-source Python. Especially, following tasks are included:

Parametrization of the phase-field model from molecular dynamics (MD) simulations.
Phase-field simulations of domain evolution in ferroelectric materials.
Phase-field simulations of domain switching under applied external electrical and mechanical fields.
Exploring influence of defects on domain evolution/switching.
Visualization of simulated results using open-source Python.

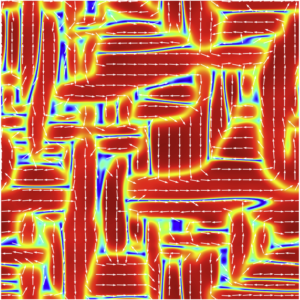
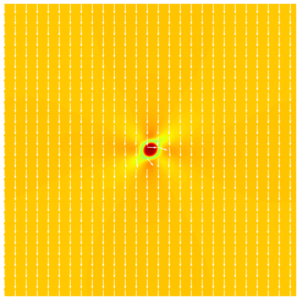
Starting the evolution from an initial random polarization state leads to the characteristic domain boundary patterns in Fig 3.

Fig. 3: Domain formation in 2D single crystal, leading to both 180° and 90° domain walls. Colours represent the magnitude of a polarization vector (nondimensionalized), white arrows represent the direction of a polarization vector. Images show the evolution under zero external strain and field from a random initial polarization distribution (simulation box: 64×64 nm², 512×512 grid points).

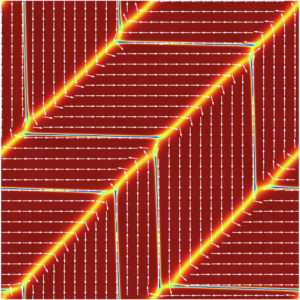
Switching of a uniform polarized crystal is possible either by applying a high electric field, or by an external mechanical stress, which favours one of the tetragonal polarization domains. The nucleation of a stress induced new domain in a homogeniously polarized involves wedge-like structures similar as in mechanical twinning (Fig. 4).

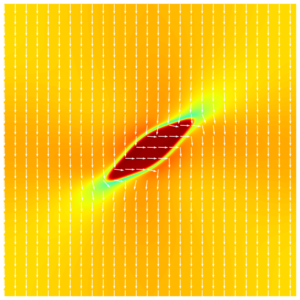
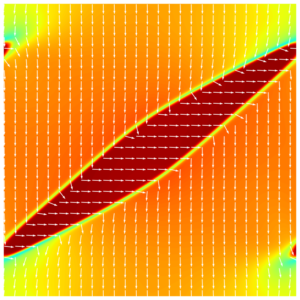
Fig. 3: Polarization switching with nucleus subjected to a compressive applied strain field of -0.3% in the y-direction Colours represent the magnitude of a polarization vector (nondimensionalized), white arrows represent the direction of a polarization vector (simulation box: 120×120 nm², 320×320 grid points).

Also, the evolution of 90° walls in 3D using the Python-FFT solver:

Contacts

Dilshod Durdiev (dilshod.durdiev@fau.de)

Dr. Frank Wendler (frank.wendler@fau.de)

Literature – Project based

T. Tsuzuki, Sh. Ogata, R. Kobayashi, M. Uranagase, S. Shimoi, D. Durdiev, F. Wendler. Vacancy-assisted ferroelectric domain growth in BaTiO3 under an applied electric field: A molecular dynamics study. Journal of Applied Physics 131, 194101, 2022.
D. Durdiev and F. Wendler. An effective Fourier spectral phase-field approach for ferroelectric materials. Computational Materials Science 218, 2023.

Literature – Other works

M. Kamlah. Ferroelectric and ferroelastic piezoceramics – modeling of electromechanical hysteresis phenomena. Continuum Mechanics and Thermodynamics volume 13, p. 219–268, 2001.
L.Q. Chen. Phase-Field Models for Microstructure Evolution. Annual Review of Materials Research 32, p. 113-140. 2002 .
S.B. Biner. Programming phase-field modelling. Springer Cham. 2017.